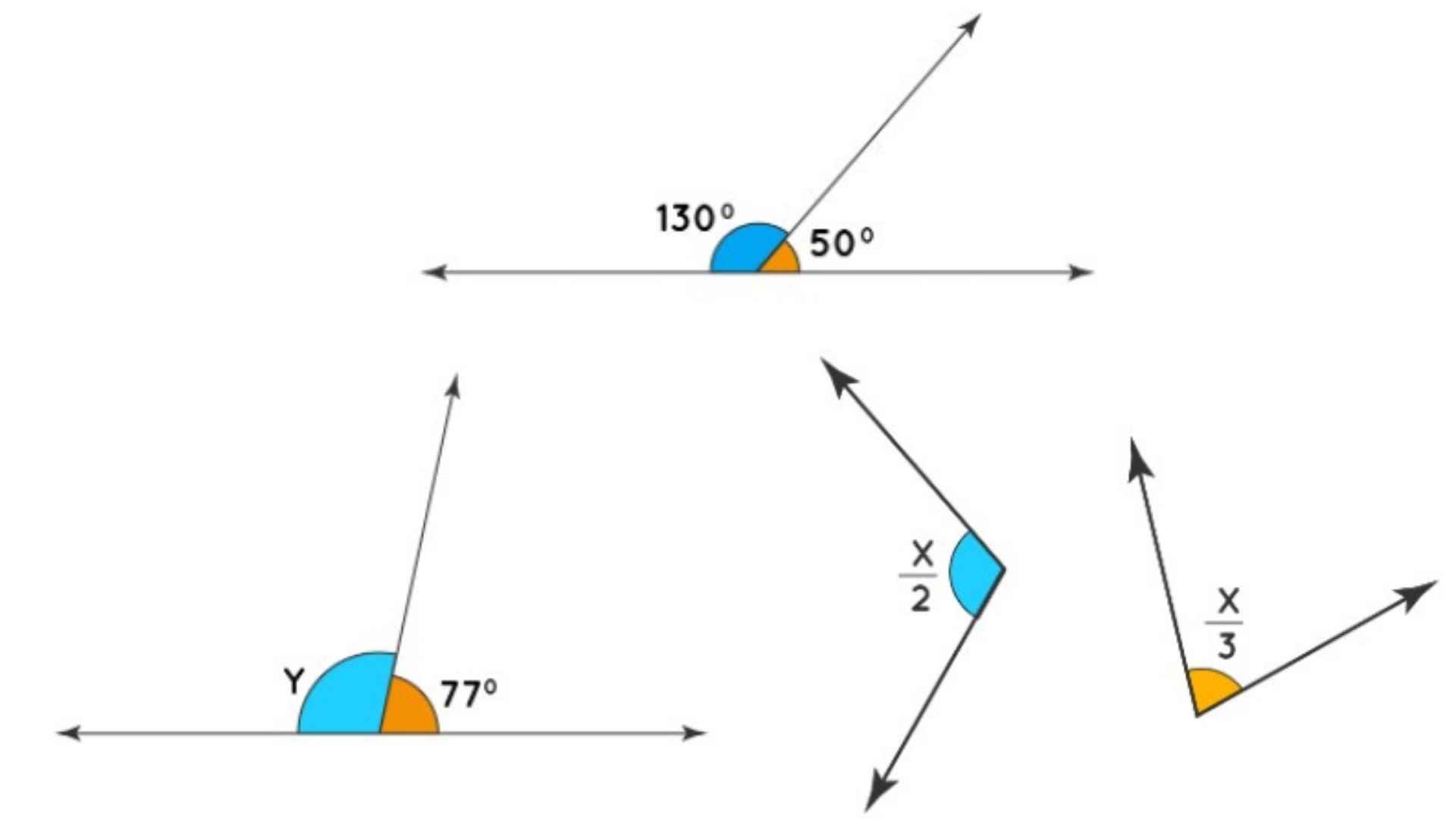
When the sum of a pair of angles is equal to 180 degrees, the angles are known as supplementary angles. Those two angles are considered as supplements to each other. Through this article, we will discuss and learn about supplementary angles and how they are different from complementary angles.
A straight line is formed when the supplementary angles are put together. We can also say that angle A and angle B are supplementary if angle A + angle B = 180 degrees.
Let us take an example to understand the concept of these angles.
Given that angle 1 = 60 degrees, and angle 2 = 120 degrees. The sum of angle 1 and 2 = 60 + 120 = 180 degrees. Therefore, the angles 1 and 2 are supplementary.
Table of Contents
Adjacent and Non-Adjacent Supplementary Angles:
There can be two types of supplementary angles- adjacent and non-adjacent angles. The following points:
- Adjacent Supplementary Angles: If we see that any two supplementary angles have a common vertex and a common arm, then those angles are considered to be adjacent angles.
- Non-Adjacent Supplementary Angles: As the name suggests, the supplementary angles that are not adjacent to each other are known as non-adjacent angles.
How to Find the Supplement of an Angle?
By now. We have learned that when two angles add up to 180 degrees, then those angles are said to be supplements to each other. If the sum of two angles is equal to 180 degrees, then the value of one of those two angles can be calculated by subtracting the other angle from 180. Therefore, the supplement of y° = (180 – y) °.
Let us take an example.
The value of angle y = 70°. Hence, the supplement of angle y = (180-70) ° = 110°.
Complementary Angles:
As per the definition, if the sum of two angles is equal to 90 degrees, then the angles are known as complementary angles. For example, if angle A and angle B add up to 90 degrees, then the angles are called complementary angles.
Let us take an example.
Given that angle 1 = 60 degrees, and angle 2 = 30 degrees. If we add up angle 1 and angle 2, i.e., 60° + 30° = 90°. The sum is 90 degrees, therefore, angles 1 and 2 are complementary angles.
Difference Between Complementary and Supplementary Angles:
The angles that are complementary and supplementary, exist in pairs. When these angles add up to 180 degrees, then the complementary angles add up to 90 degrees. One of the practical applications of such angles is crossroads. Some differences between complementary and supplementary angles are:
- In the case of complementary angles, if the sum of any two angles is equal to 90 degrees, then the angles are called complementary, whereas, if the sum of any other two angles is equal to 180 degrees, then those angles are known as supplementary angles.
- For complementary angles, the complement of angle x is (90°-x). Besides, for supplementary angles, the supplement of an angle x is (180°-x).
- ‘S’ stands for supplementary angles, and the same ‘S’ stands for a straight line as well. Therefore, it would be easier for you to remember that when these angles are put together, they form a straight line.
- ‘C’ stands for complementary angles and ‘C’ also stands for a corner. Therefore, when complementary angles are put together, they create a corner(right) angle.
To know more about supplementary and complementary angles, visit Cuemath to book a free session
Visit for more articles